动态规划 砖块合并,深入解析动态规划在砖块合并问题中的应用

深入解析动态规划在砖块合并问题中的应用

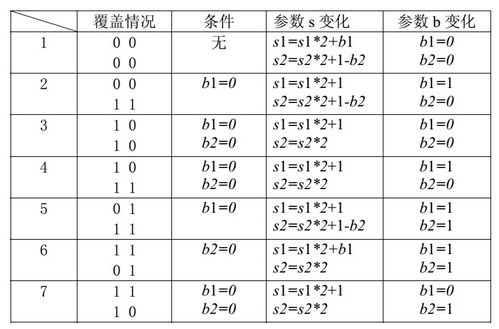
动态规划（Dynamic Programming，简称DP）是一种强大的算法设计技术，它通过将复杂问题分解为一系列简单的子问题，并存储这些子问题的解来避免重复计算，从而提高算法的效率。本文将深入探讨动态规划在砖块合并问题中的应用，分析其原理和实现方法。

一、砖块合并问题的背景

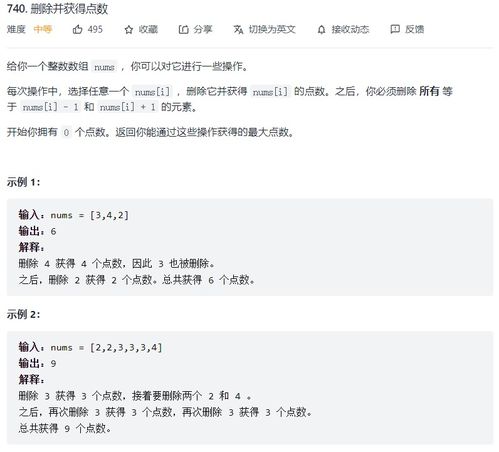
砖块合并问题是一个典型的动态规划问题。假设我们有一系列砖块，每个砖块都有一个特定的重量和体积。我们的目标是按照一定的顺序将这些砖块合并，使得合并后的总体积最小。这个问题在实际应用中有着广泛的应用，如物流优化、资源分配等。

二、动态规划在砖块合并问题中的应用原理

动态规划在砖块合并问题中的应用原理可以概括为以下两点：

最优子结构：砖块合并问题的最优解包含其子问题的最优解。这意味着，如果我们能够找到合并前k个砖块的最优解，那么我们可以通过合并第k+1个砖块来得到合并前k+1个砖块的最优解。

重叠子问题：在求解砖块合并问题时，相同的子问题会被多次求解。动态规划通过存储每个子问题的解，避免了重复计算。

三、动态规划在砖块合并问题中的实现方法

以下是动态规划在砖块合并问题中的实现方法：

定义子问题：将砖块合并问题分解为规模较小的子问题。例如，我们可以将问题分解为合并前k个砖块的最优解。

建立状态转移方程：确定问题的状态，并找到状态之间的转移关系。在本问题中，状态可以表示为合并前k个砖块的最优解，状态转移方程可以表示为：dp[k] = min(dp[i] + dp[k-i])，其中i为合并砖块的起始位置。

初始化：初始化问题的边界状态。在本问题中，当合并的砖块个数为0时，最优解为0。

计算顺序：确定计算状态的顺序。在本问题中，我们可以按照自底向上的顺序计算状态，即先计算合并前k个砖块的最优解，再计算合并前k+1个砖块的最优解。

计算最终结果：使用已计算的子问题的结果来计算原问题的解决方案。在本问题中，最终结果即为合并所有砖块的最优解。

四、动态规划在砖块合并问题中的示例代码

以下是一个使用动态规划解决砖块合并问题的Python代码示例：

```python

def brick_merge(bricks):

n = len(bricks)

dp = [0] (n + 1)

for i in range(1, n + 1):

for j in range(i):

dp[i] = min(dp[i], dp[j] + dp[i - j - 1])

return dp[n]

示例

bricks = [2, 3, 4, 5]

print(brick_merge(bricks)) 输出：6

动态规划在砖块合并问题中的应用，充分展示了其解决复杂问题的能力。通过将问题分解为一系列简单的子问题，并存储子问题的解，动态规划有效地避免了重复计算，提高了算法的效率。在实际应用中，我们可以根据具体问题调整动态规划的方法，以解决更多类似的问题。